Auf unser Video zum Thema „Delta“ (zu finden hier) hatten uns einige Reaktionen erreicht, auf die wir in einem weiteren Video eingegangen sind und auch in folgendem Artikel nochmals behandeln werden.
Natürlich sei das Delta die Gewinnchance – so zumindest ein Kommentar, der uns erreicht hat – und schließlich handele er schon seit 20 Jahren Optionen und habe damit bisher immer gute Erfahrungen gemacht. Im letzten Artikel (und einem Video auf unserem Youtube Kanal) zum Thema Delta hatten wir relativ ausführlich erklärt, warum das Delta eben nicht die Gewinnwahrscheinlichkeit darstellt und was der echte Hintergrund des Deltas ist. Trotzdem gab es dazu einige Kritik und auf einige dieser Punkte wollen wir jetzt noch einmal eingehen in diesem Artikel. Unter anderem hieß es in einem Kommentar, wenn man bei einem Strike die Delta Werte auf der Call und auf der Put-Seite addieren würde, dann würde man auf 1 kommen. Und da das 100 Prozent ergäbe, wäre das natürlich die Wahrscheinlichkeit.
Jetzt könnte man ganz einfach sagen: Nicht jeder Wert, der in Addition 1 ergibt, hat irgendwas mit Wahrscheinlichkeit zu tun – aber so einfach wollen wir es uns an dieser Stelle nicht machen, sondern steigen jetzt wirklich noch einmal mathematisch exakt in das Thema Delta ein. Das Schöne ist, daß das Delta eben mathematisch berechnet wird. Da gibt es eine klare Formel und Mathematik lügt nun einmal nicht. Es gibt keine zwei Meinungen dazu ob 2+2 vier ergibt oder nicht, das ist eindeutig und beim Delta ist es genauso.
Rein mathematisch betrachtet handelt es sich beim Delta um die erste Ableitung des Optionspreises. Wahrscheinlich haben sich die allermeisten von uns nach dem Ende ihrer Schulkarriere nicht mehr mit dem Thema Ableitungen und Kurvendiskussion befassen dürfen, deswegen noch mal kurz zur Erinnerung: Wenn wir eine Kurvenfunktion haben (und es geht um diese Kurvenfunktion des Optionspreises), dann läßt sich hier eine erste Ableitung (f‘) berechnen. Diese Ableitung gibt ganz einfach die jeweilige Steigung dieser Kurve in einem Punkt an. Das ist mathematisch relativ abstrakt formuliert, aber wenn wir das auf den Optionspreis anwenden, dann ergibt sich eben die Veränderung des Optionspreises im Verhältnis der Veränderung des Basiswertes. Sprich, der Basiswert steigt oder fällt um einen Dollar, ein angenommenes Delta von 0,3 bedeutet dann eben, daß sich der Optionspreis in diesem Fall um 30 Cent verändert. Wenn wir also die Delta-Werte im Sinne der Kurvendiskussion lesen, dann wird auch völlig klar, warum diese Werte immer zwischen 0 und 1 liegen müssen. Eine Kurve kann entweder gar nicht steigen, dann ist die Steigung (=Delta) eben 0, oder eine Kurve kann senkrecht steigen, dann ergibt sich ein Wert von 1. Werte dazwischen sind natürlich möglich und da eine Kurve nicht nur steigen, sondern auch fallen kann, gibt es selbstredend auch negative Werte bis hin zu -1. Rein mathematisch kann es also gar nicht anders sein, als daß die erste Ableitung dieser Kurvenfunktion Werte zwischen 1 und 0 bzw. 0 und -1 annimmt. Das hat überhaupt nichts mit Wahrscheinlichkeiten zu tun. An jedem Punkt der Kurve wird einmal die Callseite betrachtet und auf der anderen Seite die Puts, und die Wertveränderung der beiden Optionen ist natürlich gegenläufig. Logischerweise muß das in Addition eins ergeben in Bezug auf das Delta. Es bleibt also festzuhalten, daß das Delta ganz einfach angibt, wie sich der Wert einer Option ändert im Verhältnis zur Wertänderung des Basiswertes. Das – und NUR das – stellt Delta per Definition dar. Ende der Diskussion.
Für alle, die sich mit diesen Tatsachen nur schwer anfreunden können, vielleicht noch ein kleiner Blick zurück in die Optionsgeschichte, in die Geschichte der Optionspreis Berechnung. Wir sprechen hier über die sogenannte Black-Scholes Formel zur Optionspreis Berechnung, die 1974 entwickelt wurde von den drei Wirtschaftswissenschaftlern Fisher Black, Myron Scholes und Robert Merton (wofür 20 Jahre später 1997 auch der Wirtschaftsnobelpreis vergeben worden ist). Auf dieses Optionspreis Modell nach Black-Scholes geht auch die Berechnung des Deltas zurück. Das Modell ist zwar immer noch in Gebrauch, aber wie sich zwischenzeitlich herausgestellt hat, gibt es dort einige Ungereimtheiten, einige Fehlannahmen, die so keinen Bestand mehr haben. Zu nennen ist, daß die Volatilität als konstant angenommen wird, und zwar sowohl über verschiedene Laufzeiten, als auch über die verschiedenen Strikes. Daß dies anders ist, weiß man inzwischen. Ein weiterer Punkt ist, daß das Modell auf der Berechnung der Optionspreise für Optionen europäischer Ausübungsart beruht, die allermeisten heutzutage gehandelten Optionen aber amerikanischer Ausübungsart sind. Kurz erklärt, die Optionen europäischer Ausübungsart (die nichts mit Europa zu tun haben oder mit in Europa gehandelten Aktien) können nur am Ablauftag ausgeübt werden, während Optionen amerikanischer Ausübungsart auch während der Laufzeit ausgeübt werden können. Ein Video zu diesem Thema ist auf unseren Youtube Kanal zu finden.
Während also in dem Optionspreismodell nach Black-Scholes in Bezug auf das Delta überhaupt nicht von Eintrittswahrscheinlichkeiten in the money oder out of the money die Rede ist, geht es bei der Berechnung der Wahrscheinlichkeiten um ganz andere Faktoren. Das ist mathematisch betrachtet eine vollkommen andere Formel. Das verlinkte PDF von Morgan-Stanley stellt die Vorgehensweise zur Berechnung der Eintrittswahrscheinlichkeiten dar; beschäftigt Euch gerne mit dieser Berechnungsmethode, die auch Einzug gehalten hat in professionelle Optionssoftware.
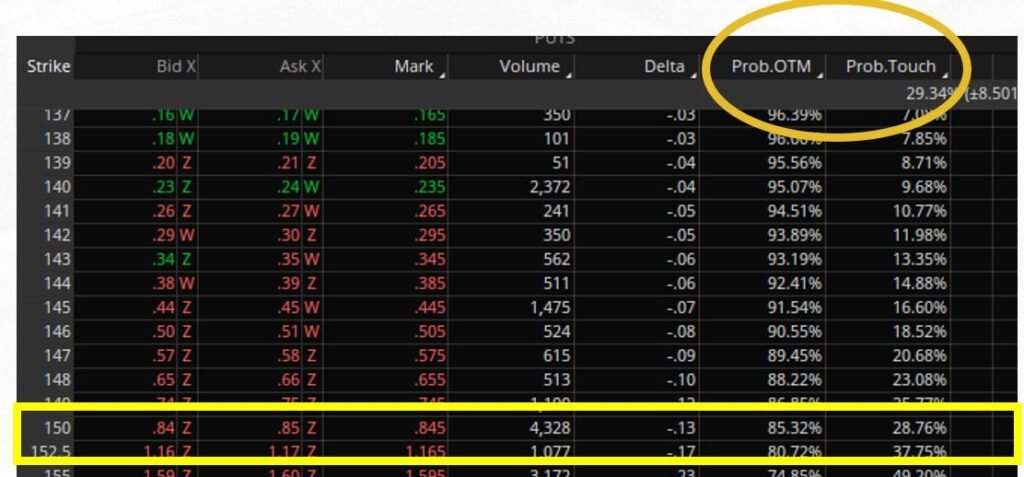
An dieser Stelle sollen nochmals gegenübergestellt werden die Delta-Werte mit den Wahrscheinlichkeiten nach dieser Berechnungsmethode. Wie in diesem Beispiel sehr schön zu sehen, beträgt die Wahrscheinlichkeit korrekt berrechnet 85,3%; orientiert man sich am Delta, kommt man auf 87%. Nun man man uns hier Erbsenzählerei unterstellen, aber genau deswegen haben wir im letzten Artikel und Video auch erwähnt, daß das Delta als Faustformel – als Pi mal Daumen, als grobe Richtschnur – durchaus anwendbar ist. Verfügt man also nicht über professionelle Optionssoftware, dann ist es vollkommen in Ordnung, wenn man sich näherungsweise mit dem Delta befaßt und anhand des Deltas ungefähr abschätzt, wie wahrscheinlich ein Eintritt sein könnte. Mathematisch korrekt ist es allerdings trotzdem nicht.
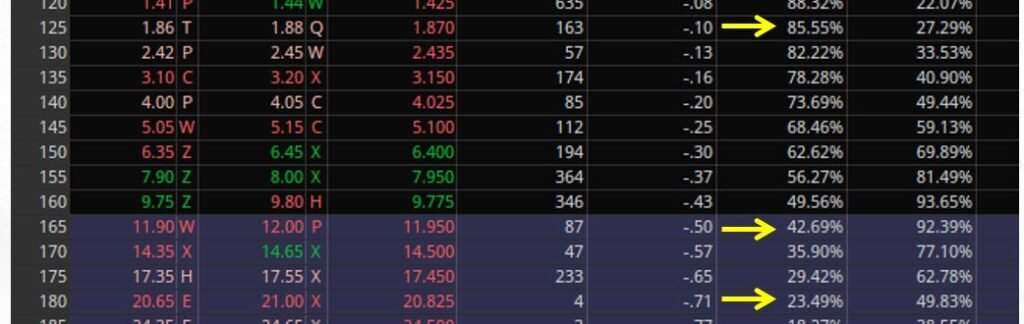
Dieser Unterschied wird um so stärker, je länger die Laufzeit ist. Je niedriger die Volatilität und je kürzer die Restlaufzeit der gewählten Option, um so näher kommt man mit dem Abschätzen der Eintrittswahrscheinlichkeit anhand des Deltas der echten Wahrheit, nämlich der probability in the money oder probability out of the money. In obigem Beispiel aus einer längeren Laufzeit wird dieser Unterschied sehr schön klar. Bei einem Delta von 10 (nach der Faustformel eine Wahrscheinlichkeit von 90% für OTM) beträgt die tatsächliche Wahrscheinlichkeit OTM nur 85,55%. Bei dem Delta von 71 sind es nicht 29%, sondern ungefähr 23,5%. Sehr schön zu erkennen auch at the money, wo das Delta 50 ist (die Preisveränderung der Option also 50 Cent beträgt, wenn sich der Basiswert um einen Dollar bewegt), daß hier eine ganz abweichende probability out of the money von 42,7% vorliegt und eben nicht von 50%.
In einem weiteren Kommentar wurde hier auch noch etwas durcheinander gewürfelt, da wurde über die probability of touch gesprochen (in der Abbildung oben auch zu sehen). Diese probability of touch stellt dar, wie wahrscheinlich es ist, daß der jeweilige Strike während der Laufzeit zumindest einmal berührt wird. Da hieß es in dem Kommentar, das sei doch nur für Knockouts relevant, da diese bei Berührung während der Laufzeit verfallen würden, für Optionen sei das aber völliger Quatsch. Wir sprechen hier weder über Knockouts, noch über Zertifikate, Optionsscheine oder andere Bankenprodukte, wir reden hier ausschließlich über börsengehandelte Optionen. Und auch hier läßt sich diese Wahrscheinlichkeit eben berechnen. Ob man nun meint, daß die relevant ist – da kommt es eben ganz auf das persönliche Risikoempfinden an. Nicht jeder Trader bewahrt einen kühlen Kopf, wenn sein Shortstrike während der Laufzeit angelaufen wird. Das persönliche Trade- und Risikomanagement ist ein sehr individuelles und unterschiedliches. Wenn Dein Risikomanagement z.B. vorsieht, daß du in den Trade managend eingreifst, sobald der Shortstrike berührt wird, dann ist es sehr wohl relevant zu wissen, in wieviel Prozent der Fälle das denn passieren könnte.
Selbstverständlich können wir die Entrüstung einiger Trader nachvollziehen, die vielleicht schon seit Jahren erfolgreich traden und ihre Wahrscheinlichkeiten immer anhand des Deltas eingeschätzt haben. Die Erkenntnis, daß die mathematische Wahrheit einfach eine andere ist, sollte an sich aber gar kein Problem sein. Denn wenn Du bis jetzt erfolgreich getradet hast mit der Abschätzung der Eintrittswahrscheinlichkeit anhand des Deltas und Dein Trade- und Risikomanagement dazu paßt, dann herzlichen Glückwunsch! Never change a winning team, handele doch einfach weiter so! Nicht für jeden ist die mathematisch korrekte Auslegung so wichtig, und eines darf man auch nicht vergessen: Sowohl das Delta, als auch die Eintrittswahrscheinlichkeiten, können sich täglich ändern. Mit unterschiedlicher Volatilität, mit der Veränderung des Basiswertes, und die Kurse steigen und fallen nun einmal. Die Fälle dürften also extrem selten sein, in denen es wirklich eine wahnsinnig große Rolle spielt, ob Du jetzt um drei, vier, fünf Prozentpunkte hin oder her die Wahrscheinlichkeit zu Beginn deines Trades korrekt eingeschätzt hast. Denn wenn Dein Trade- und Risikomanagement stimmt und konsequent umgesetzt wird, dann ist eben genau das der Schlüssel zum Erfolg.



